简介

Union-find，合并-查找，这个算法是在学习Algorithms这本书的时候看到的。

用于解决的问题

假定一个学校的圈子中，有A,B,C...这些人，而A,B存在联系，B,C存在联系，若要寻找A,C是否存在联系，只要存在B这个媒介，那么就说明有联系。为了建立这样的关系网，把存在联系的人连接合并成集合，这样在判断联系时，只需要判断是否存在这个集合里即可。抽象地说，就是在一个图中划分出连通子图。

核心的方法需求

Union(p, q): 将点p和点q建立连接的方法。

Find(p): 寻找点p所在的子集。通常用Find(p)==Find(q)来判断p和q具有连通性。

基本构建思路

Quick-Find

这是最大化搜索效率的思路。在进行Union的时候会让所有的节点保存root（根节点），每次连接的时候为连通的节点设置同一个root，这样find时只需要读取root这个值即可。

图解

Java代码

缺点

如果一条很长的链被合并，可能需要大量地改变root值。

Quick-Union

这是最大化合并效率的思路。在进行Union时只保存上级节点，这样find的时候一直追溯到根节点，也能判断是否在同个子集。

此时使用类似链表的数据结构十分恰当。

图解

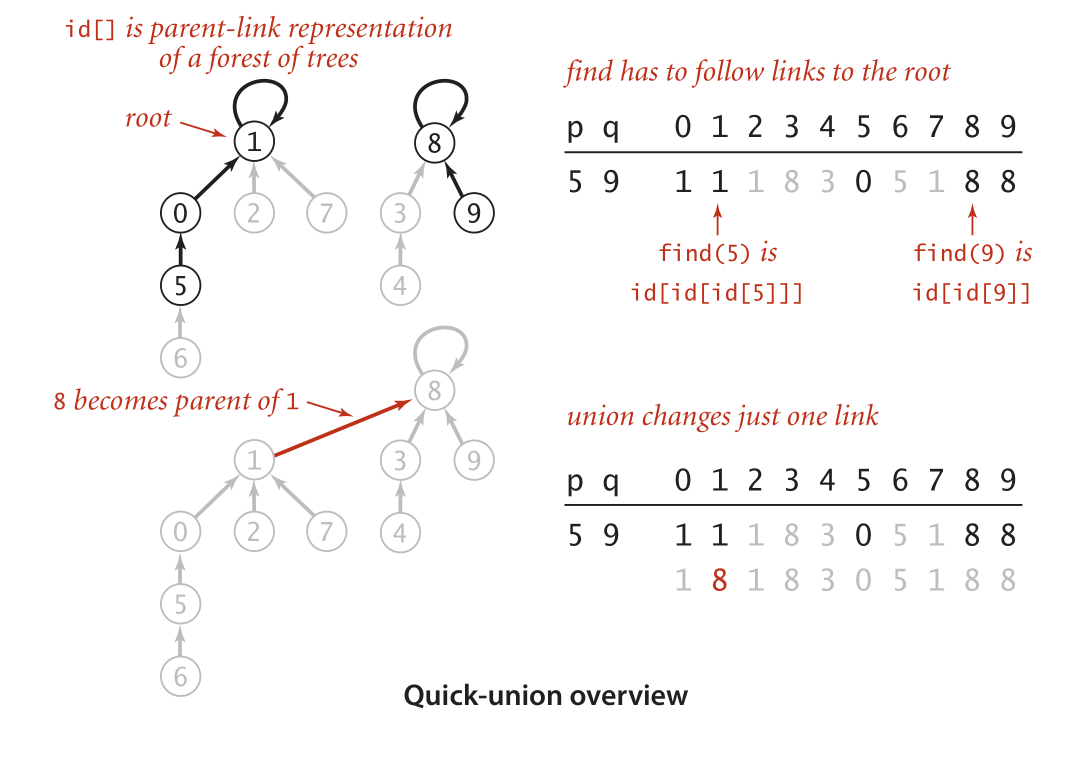
Java代码

缺点

如果有一条很长的链，查找效率会很低。

二者比较

共通点

不管是quick-find还是quick-union，算法中都有这样的共通点：

1.每次union时会判断是否同根，如果是则直接跳过。

2.在进行两个子集的union时，会连接两个子集的root。

时间复杂度比较

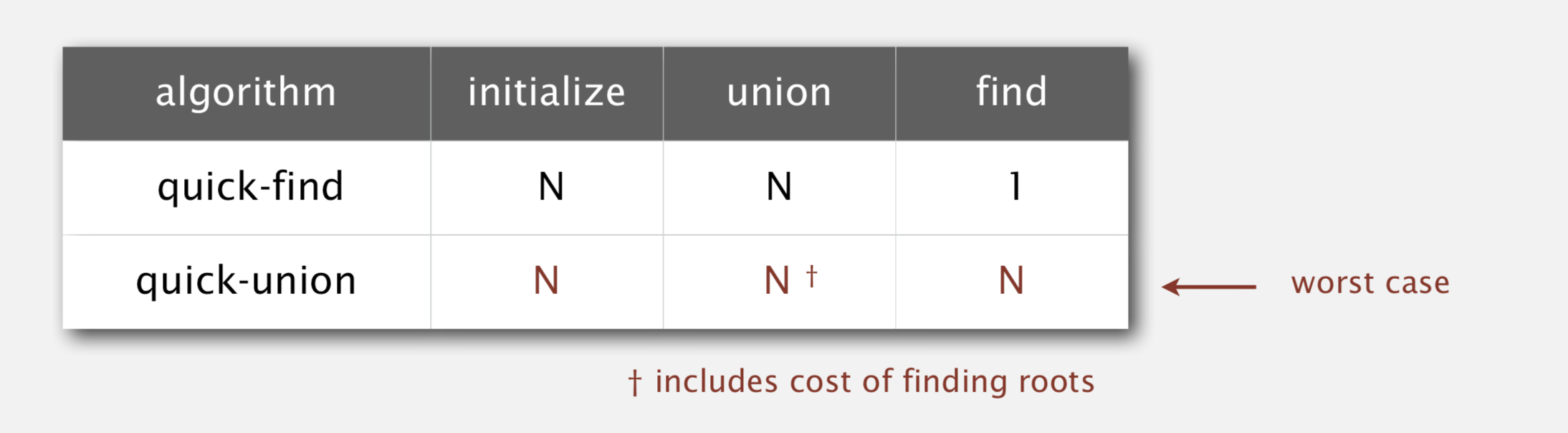
因为quick-union每次都要查找，所以在最坏情况下合并的效率跟quick-find拥有相同的复杂度，但好的情况下合并的效率会大大提高。

由于quick-union的方法更优雅，我们接下来会采用quick-union并尝试优化。

Quick-Union算法的优化

Map

因为所有的节点都有唯一的id，在我的算法中相比书中使用数组会选择使用HashMap保存节点，这样能够提高索引效率。同时，因为每个节点只有唯一的parent，而可能有多个child，且find过程中也只是追溯parent，所以只单向保存parent的id。

结构：{key: id, value: parent_id}

Weighting

Weighting，即平衡重量。基本思路是判断两个要合并的root的child数量，将小的合并到大的，这样可以避免生成长子链，然后提高查找效率。

图解

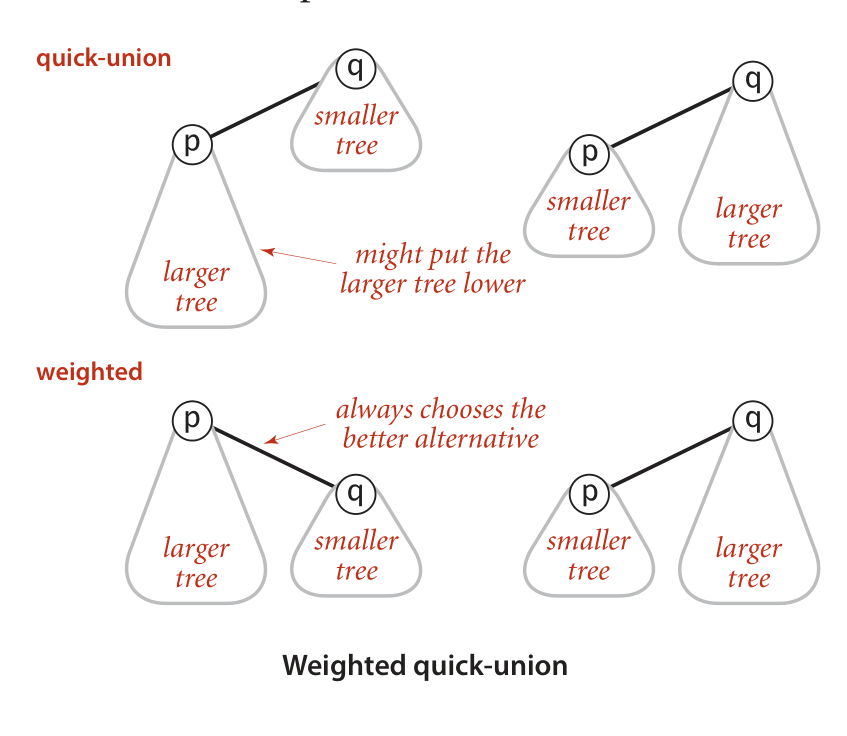
代码变动

由于每个节点只保存了parent，故无法追溯child的长度，因此每个节点新增一个size属性，每次union时将child以及其对应的子集size合并到该节点的size中。

map结构变化: {key: id, value: {parent: parent_id, size: size}}

union时： map.get([要合并的parent]).size+=map.get([被合并的child]).size +1 //+1是child本身

Path Compression

Path Compression，即路径压缩。基本思路是在每次合并的时候直接将child（的root）合并到parent的root上，这样也可以避免生成长子链。

图解

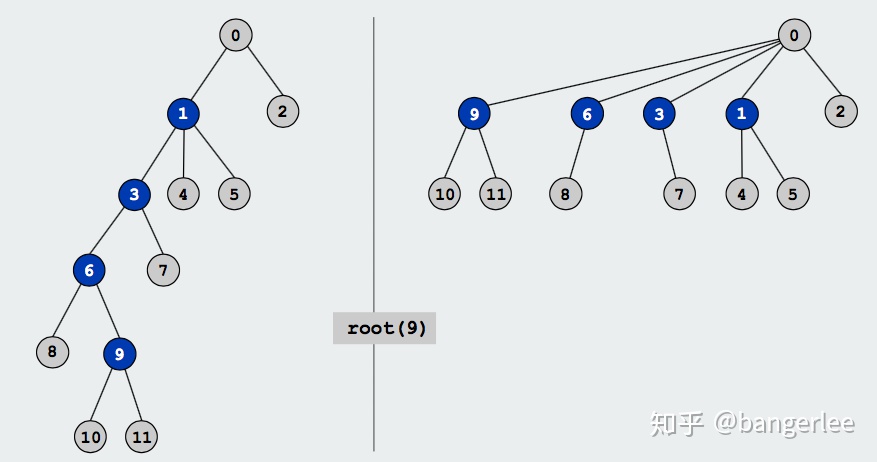
最终代码

quick-union + weighting + path compression + map

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

const map = new Map();
class Node {
    //每个节点保存的结构
    constructor(parent, size){
        this.parent = parent || null;
        this.size = size || 0;
    }
}

function union(p, q){
    if(!map.has(p)||!map.has(q)){
        //有一个不在map里，说明是游离节点，自动设为child
        if(!map.has(p)){
            var child = p, parent = find(q); //path compression 父母直接设给根节点
        } else {
            var child = q, parent = find(p);
        }
        map.set(child, new Node(parent, 0));
    } else {
        //均存在map中，需要进行weighting的两个节点
        const pr = find(p), qr = find(q), prs = map.get(pr).size, qrs = map.get(qr).size; //暂存两个节点的root
        if(pr===qr){
            //如果已经连通，不需要再连接了
            return;
        }
        if(prs < qrs){
            //把容量更小的那个设为child被合并
            var child = pr, parent = qr;
        } else {
            var child = qr, parent = pr;
        }
        //root应该都存在map中
        map.get(child).parent = parent;
    }
    if(!map.has(parent)){
        map.set(parent, new Node(parent, map.get(child).size+1)); //map中新建一个root node，root的parent设给自己
    } else {
        map.get(parent).size+=map.get(child).size+1; //合并size
    }
};

function find(p){
    if(!map.has(p)){
        return p;
    }
    while(map.get(p).parent!=p){
        //如果parent等于自己，说明已经是根节点了，否则再往上追溯一个parent
        p = map.get(p).parent;
    }
    return p;
};

function isConnected(p, q){
    return (find(p)===find(q));
}

时间复杂度

最后贴上algorithms书中的各种方法的时间复杂度：

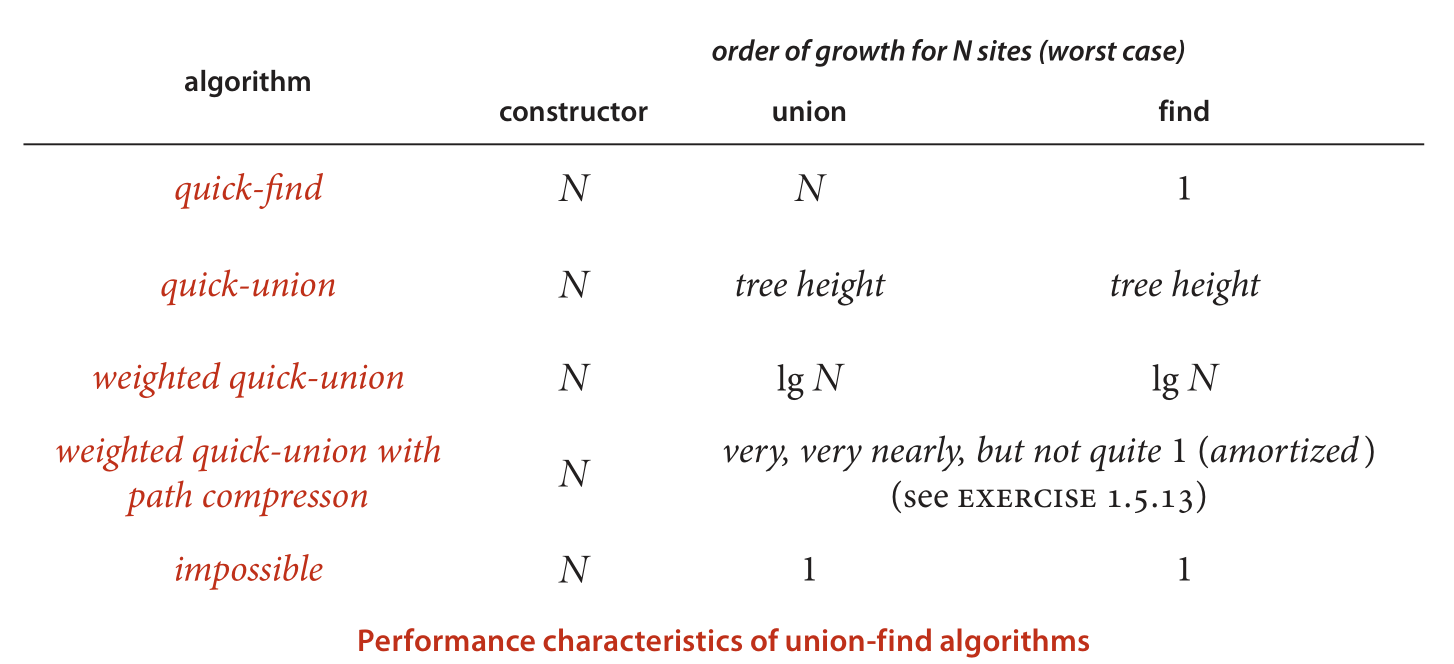
有weighting和path compression的quick union时间复杂度无限接近1。